智能建模功能简介

01数据源

1. 本地数据文件

智能建模支持txt、csv等格式的数据文件。

选择文件后，可以定义数据文件的参数配置。

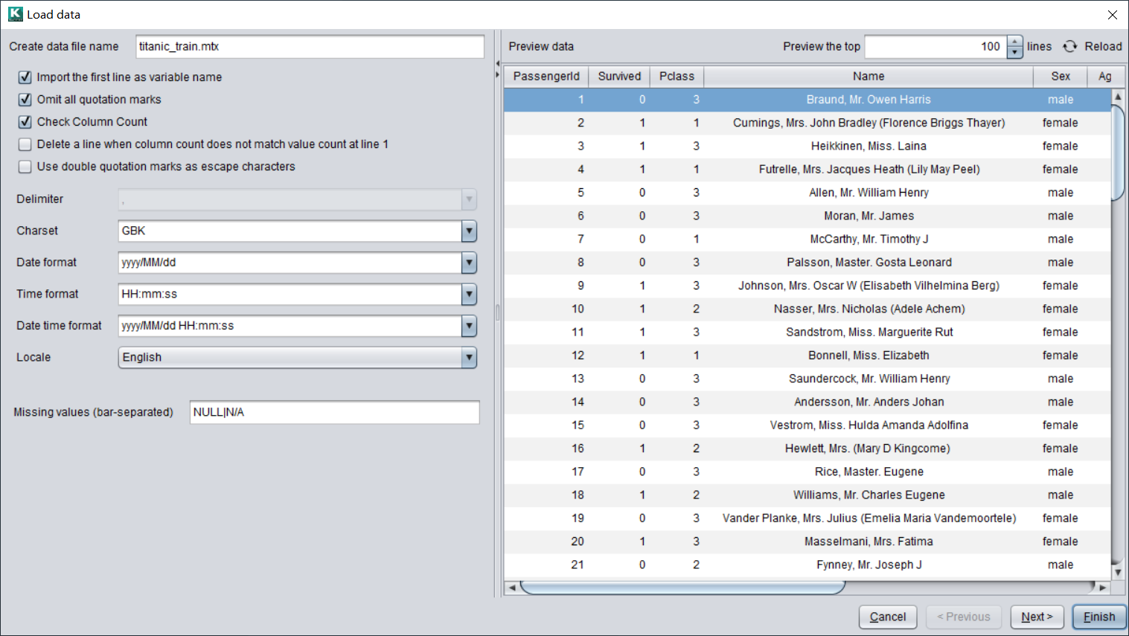
下一步，可以定义变量类型、日期格式和选出状态。

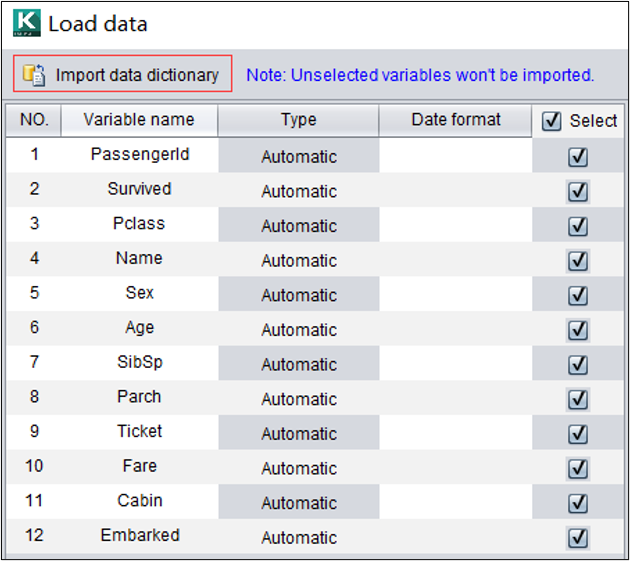
变量类型既可以自动检测，也可以导入数据字典配置。数据字典格式如下：

Name	Type	DateFormat	Used	Importance
PassengerId	Identity		TRUE	0
Survived	Binary		TRUE	0
Pclass	Categorical		TRUE	0
Name	Text		FALSE	0
Sex	Binary		TRUE	0
Age	Numerical		TRUE	0
SibSp	Categorical		TRUE	0
…	…	…	…	…

2. 数据库

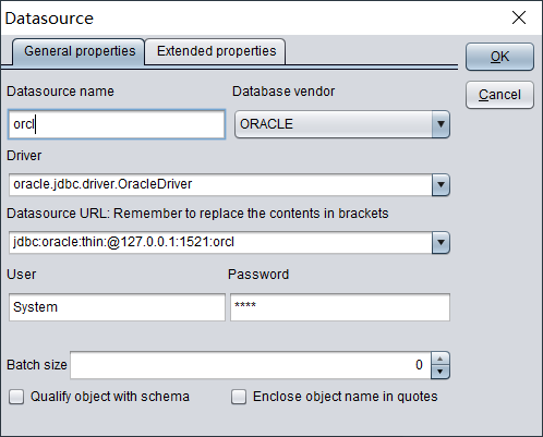
在数据源窗口中，可以定义JDBC和ODBC两种数据源连接。

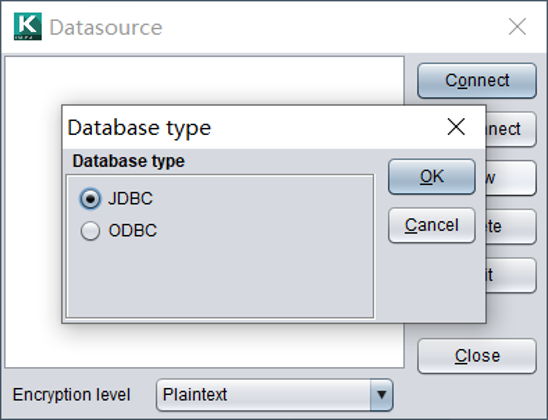
JDBC数据源

ODBC数据源

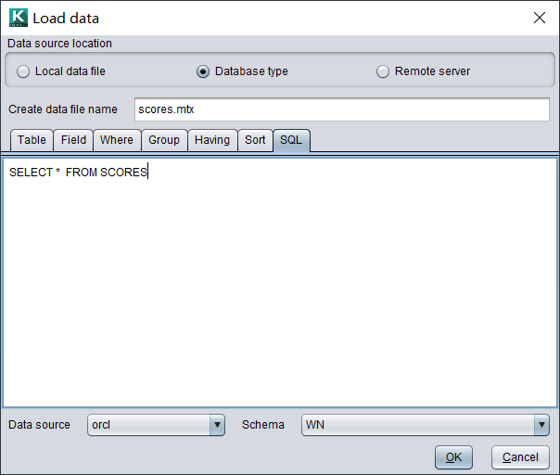
接下来可以使用配置好的数据源，编辑SQL语句进行取数。

02数据探索

1. 基本特征

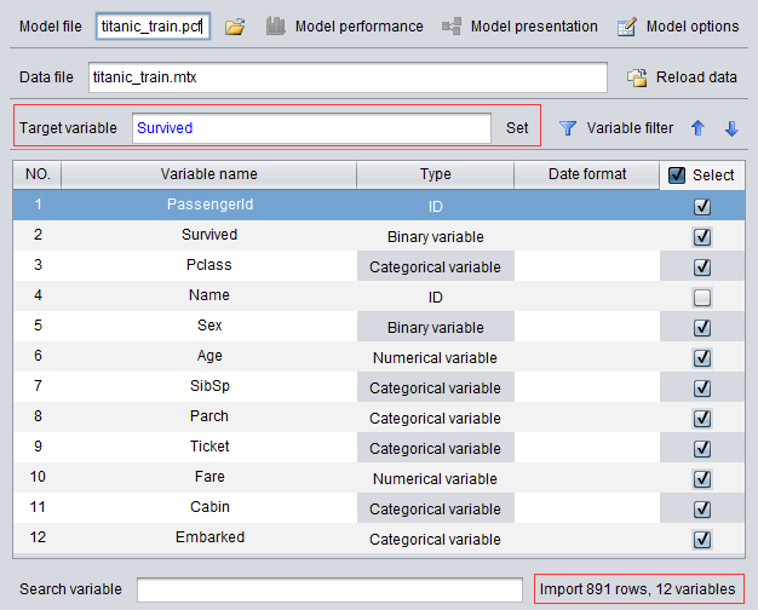
导入数据以后，显示了数据的基本特征：

目标变量是Survived（需要用户设置），有12个变量，891条记录。

自动解析了各个变量的类型和推荐的选出状态。

智能建模的变量类型有以下几种:

变量类型	描述
数值变量	取值为实数的变量
单值变量	只包含一个类别的变量（不含缺失值）
二值变量	只包含两个类别的变量（不含缺失值）
计数变量	取值为自然数的变量
分类变量	分类数大于二的变量（不含缺失值）
ID	唯一标识符
时间日期	日期、时间或日期时间变量
长文本	长度超过128字节且分类数特别多的变量

智能建模的目标变量支持二值变量、数值变量、计数变量和分类变量。

2. 离散变量统计

离散变量包括单值变量、二值变量和分类变量。

缺失率：缺失值在全部数据中的占比。
势：离散变量可取值集合的成员数量。
饼图直观显示了各分类的占比。

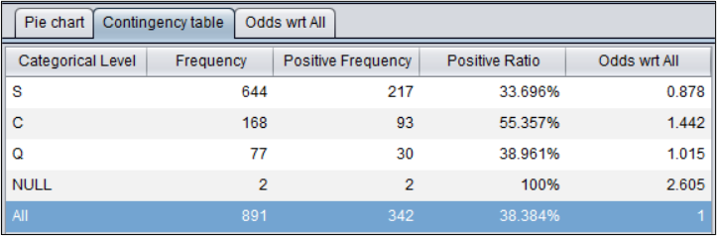
目标变量是二值变量：分组目标频数表

分组目标频数表将样本按分类值分组，观察每组样本的数量和正样本数，正样本率以及赔率（发生比）。

二值目标的正样本是指样本数较少的分类值。通过右图可以看到，在本例中正样本是目标变量值为1的记录。

目标变量的饼图

Odds wrt All 图形显示了每组样本的赔率和总的赔率。样本较少的分类（样本数少于100个）不进行绘制。

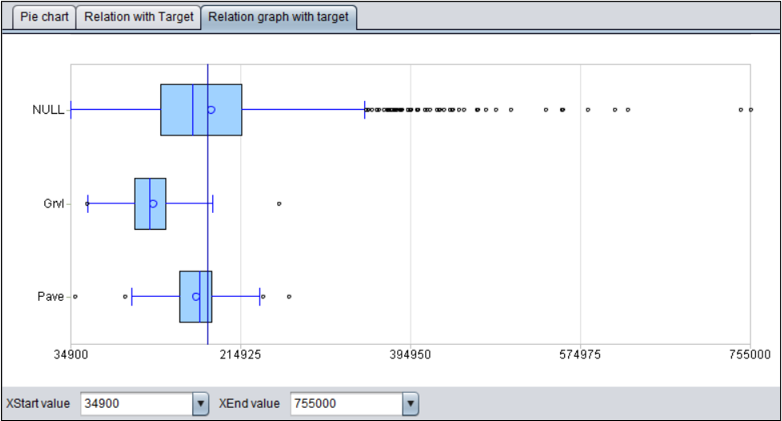
目标变量是数值变量：分组目标统计量，分组目标统计图

分组目标统计量将样本按分类值分组，观察每组样本的统计量。包括：频率，平均值，标准差，中位数，最小值和最大值以及Z-STAT。

分组目标统计图，使用箱线图的形式，更直观的表现了每组样本的分布情况。箱线图可以用来标记异常值。

3. 连续变量统计

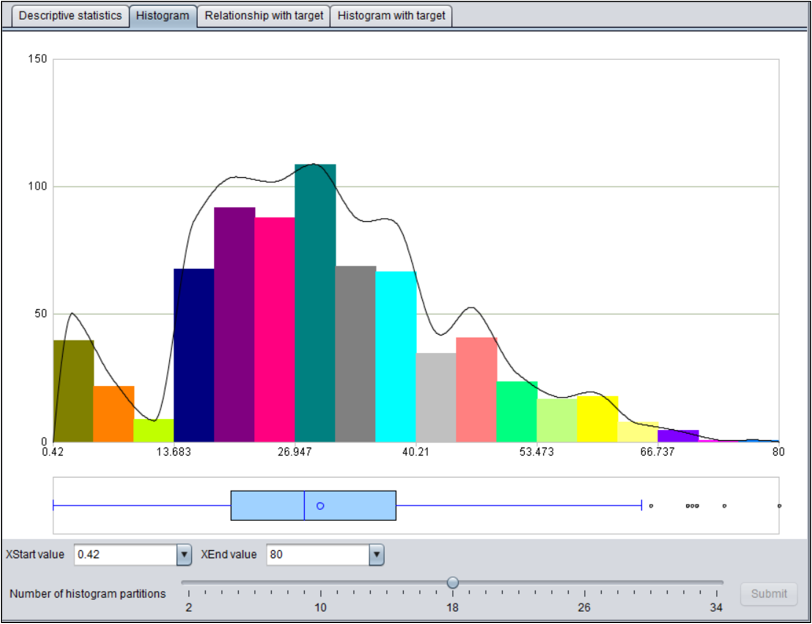
连续变量包括数值变量、计数变量和时间日期变量。

描述性统计量显示了数据的基本统计信息。

频数分布图，绘制了频数分布直方图，正态分布曲线，以及箱线图。

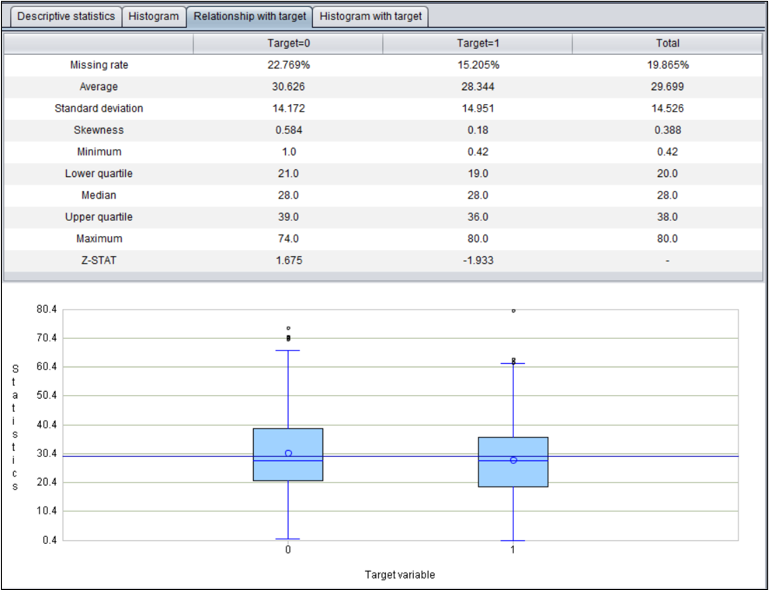
目标变量是二值变量：分组描述性统计量

分组描述性统计量，将样本按目标变量值分组，分别进行统计，并绘制相应的箱线图。

目标变量是二值变量：分组频数分布图

分组频数分布图，将每个区间的样本按目标变量值分组，频数用不同颜色显示。

目标变量是数值变量：目标变量相关系数

Pearson相关系数：用于描述两个连续变量之间的线性相关性。

Spearman秩相关系数：用于描述两个连续变量之间的等级相关性。

相关系数的绝对值越大，表示两个变量的相关性越大。

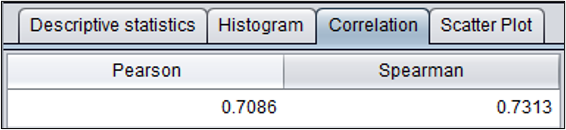
上图是地下室面积和房价之间的相关系数。可以看到两者有很强的相关性。

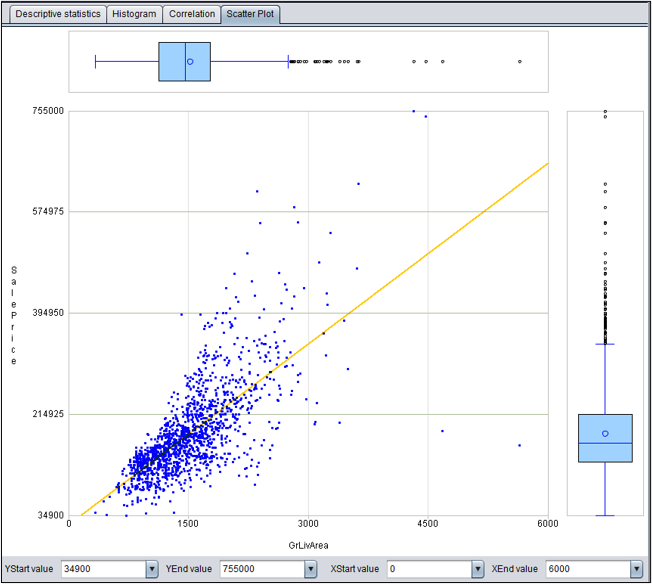
目标变量是数值变量：单因素散点图

单因素散点图直观的展现了当前变量（地下室面积）和目标变量（房价）相关的分布情况。其中黄线为回归线。

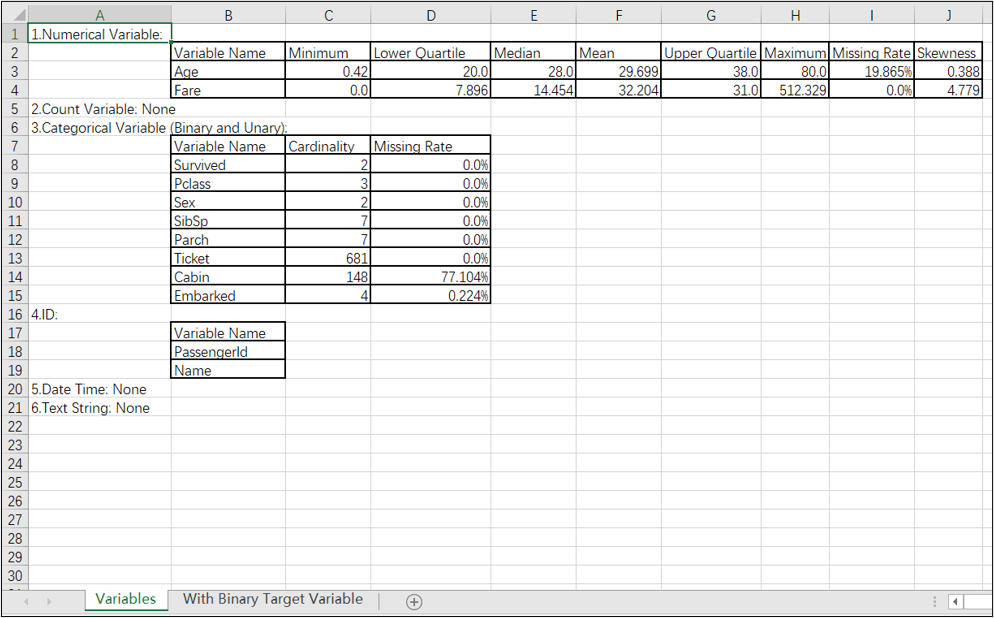
4. 数据探索报告

提供导出数据探索报告到excel文件的功能。第一页是各类变量的基本信息：

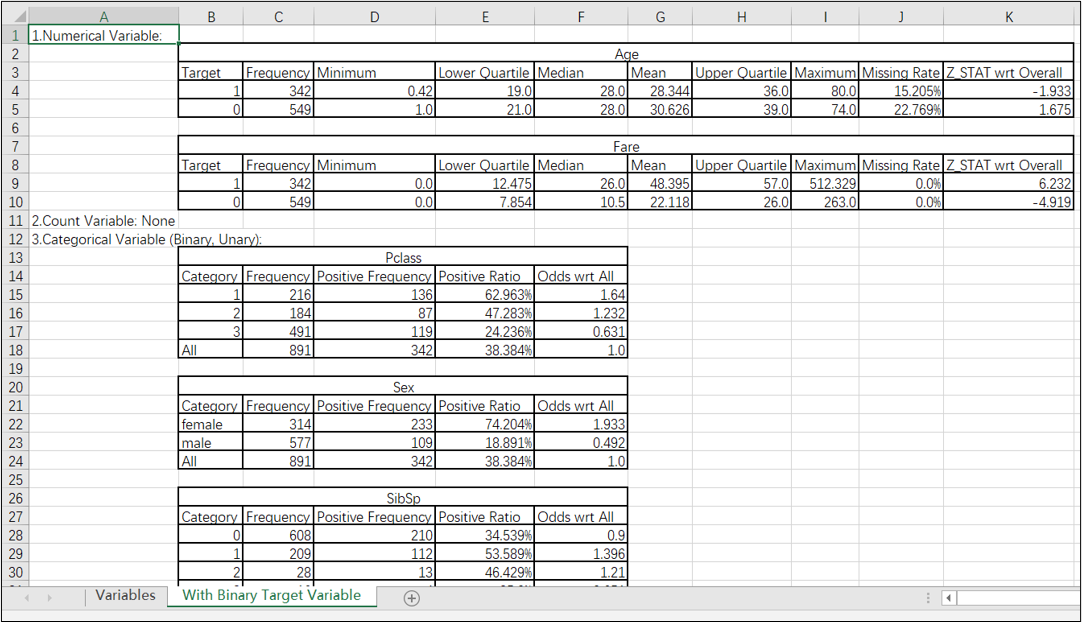
第二页是各类变量与目标变量的关联性：

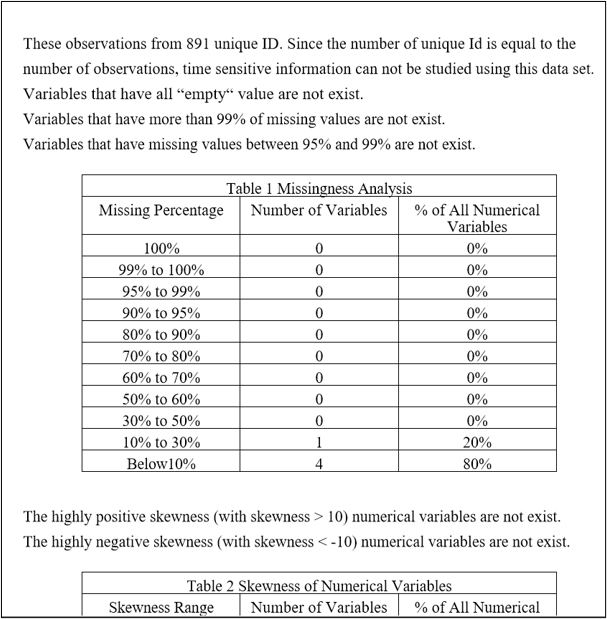
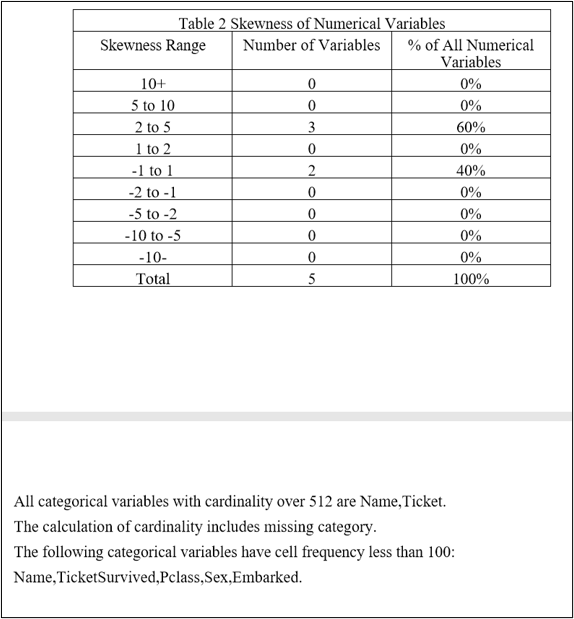
5. 数据质量报告

提供导出数据质量报告到pdf文件的功能。部分内容如下：

03预处理

1. 自动预处理

智能建模的预处理过程集成在建模的流程中，一键式自动预处理。

2. 预处理报告

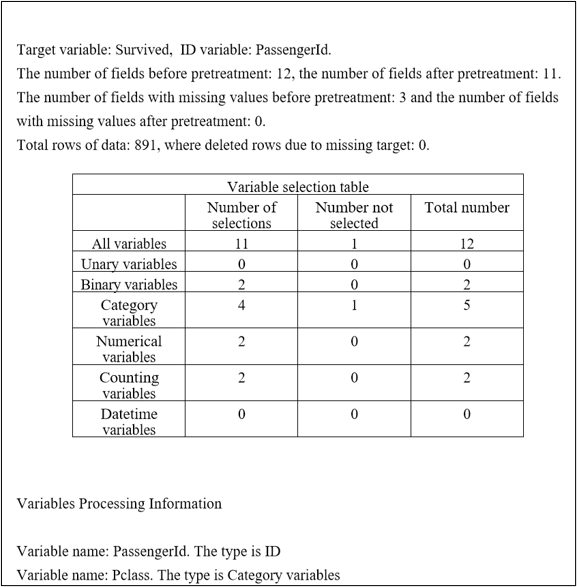
建模结束后可以导出模型报告，描述了预处理执行了哪些动作。部分内容如下：

3. 预处理流程

（1）检查变量值域

检查并记录所有变量的值域，若测试数据出现训练数据没有的分类或者超出数值范围，进行针对性的处理。

（2）时间日期变量处理

检查所有时间日期型变量，创建若干常用的衍生变量。并检测时间日期变量的关联性，创建多日期联动的衍生变量。

（3）缺失值信息提取

若数据存在缺失值，提取并记录缺失值模式，将缺失值所表现出的行为特征转换为衍生变量加以利用。

（4）缺失值填补

若数据存在缺失值，利用简单或个性化智能算法，填补缺失值。

（5）分类变量降噪

针对分类变量可能存在的噪音，例如极少数分类，异常分类，疑似错误分类等情况，进行针对性处理。

（6）分类变量数值化

将分类变量转换为可正常进行运算的数值型变量。主要方式是dummy variable和平滑化，由算法智能判断。

（7）纠偏

针对部分存在正态性假设的模型，对高偏态变量进行数学变换，使偏度回到0附近，满足模型假设。

（8）异常值处理

探测并识别可能存在的异常值，并进行针对性处理。

（9）变量筛选

以较宽松的门槛，剔除掉对建模无用的变量，降低时间成本和模型复杂度。

（10）标准化/归一化

数据标准化/归一化，消除口径差异。有利于神经网络等模型的寻优求解。

（11）平衡样本

对于二分类数据，若正负样本比例严重不均衡，会按照指定的比例配平，并智能重采样建模。

4. 手动预处理

选择变量

根据变量类型去除一些无关的变量。例如ID和长文本，没有缺失值的单值变量等。

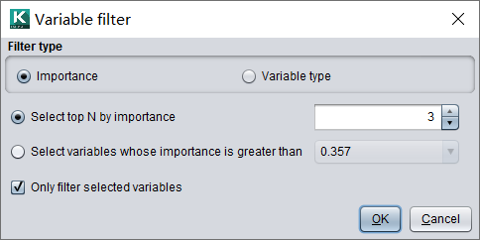
根据变量重要度筛选变量，只保留重要度较高的变量。变量重要度可以由数据字典导入，也可以通过建模得到。

衍生变量

用变量姐妹、配偶数量"SibSp"和变量父母、子女数量"Parch"相加得到家庭成员数量"Family"。可以看到家庭成员在1-3人时幸存率较高。

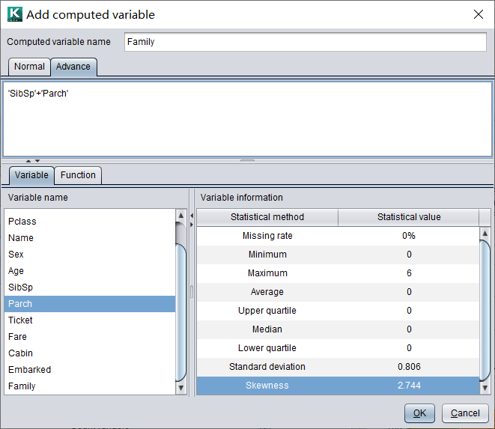
增加衍生变量Family

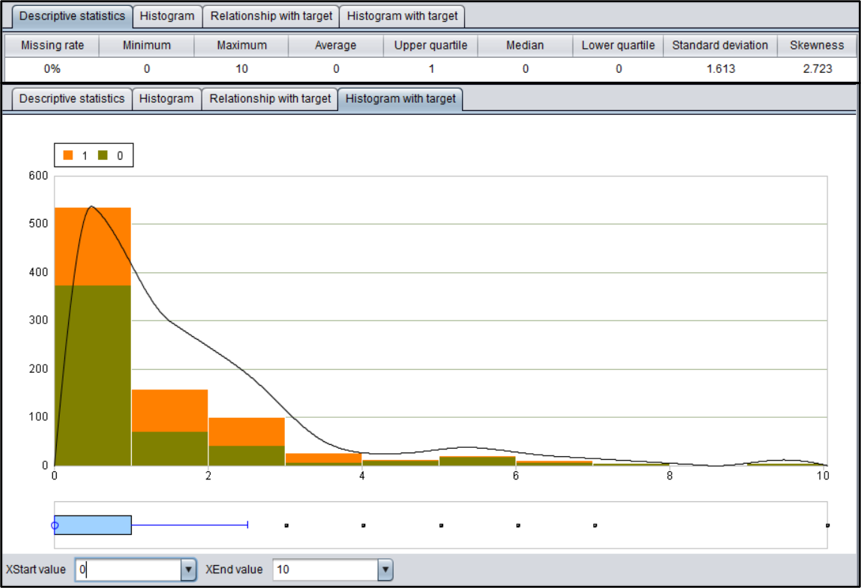
统计变量Family

可以将数值变量通过分箱离散化，转换为分类变量。以年龄为例，分为0，8，18，35，60几个年龄段，生成衍生变量，并对其进行统计。

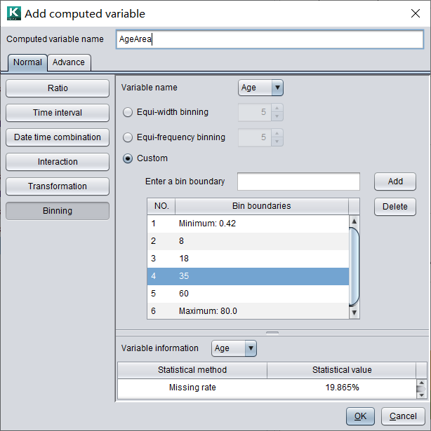
增加衍生变量AgeArea

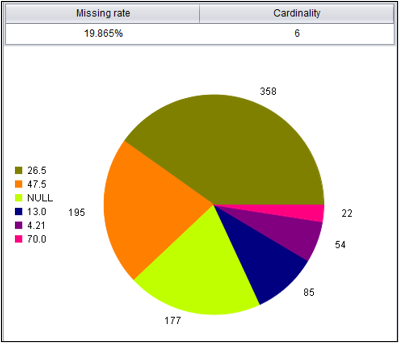
统计变量AgeArea

可以看到0-8岁的少年幸存率最高，青少年、青年和中年的区分不大，老年幸存率最低。

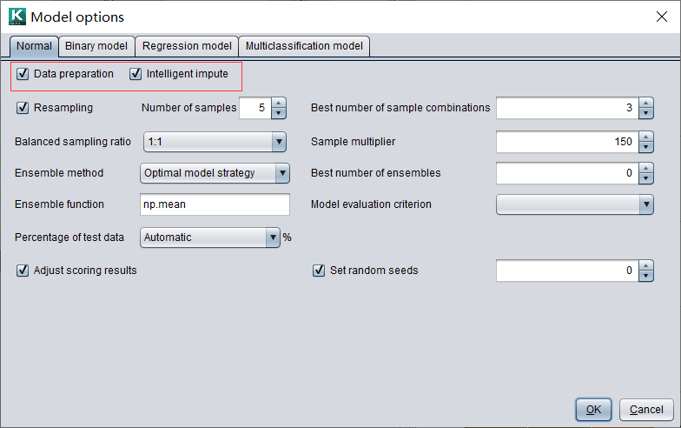
预处理选项

在模型选项中可以定义是否数据预处理和是否智能填补。

如果数据已经进行过预处理，可以取消数据预处理。

智能填补可以更好的对缺失值进行补缺，但是会消耗更多的硬件资源和时间，当数据量很大时不建议智能填补。不勾选时会进行简单填补。

04建模

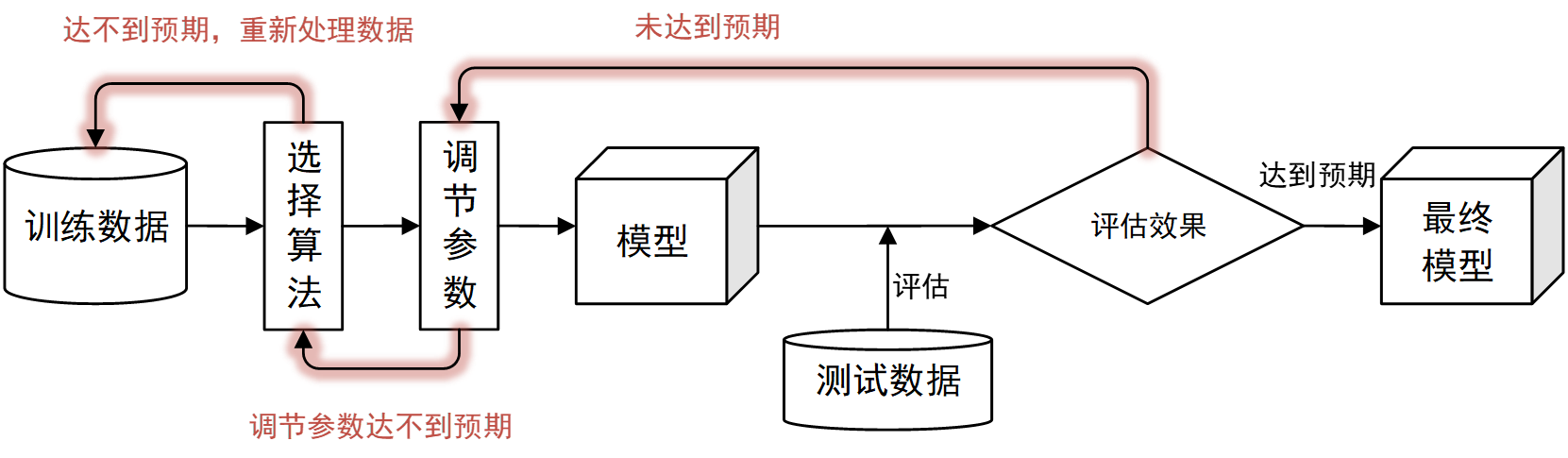
1. 建模流程

在使用传统工具时，通常需要有统计学基础的专业人员，不断选择算法，调整模型参数，最终得到符合期望的模型。建模的流程如下：

2. 智能建模

智能建模工具无须统计学知识，一键式智能建模，优选模型组合和模型参数都在内部实现。

3. 专业建模

智能建模开放了模型参数，提供给精通模型的专业用户使用。下面是模型的常规选项：

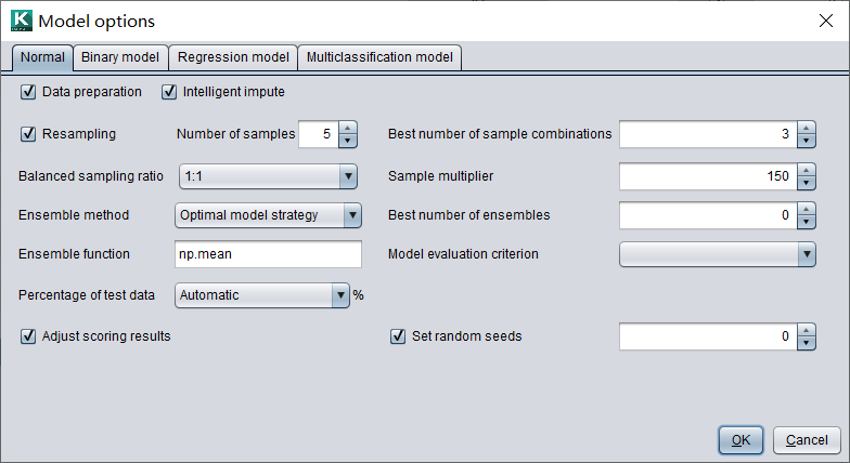
智能建模支持图中几种二分类算法模型，还可以设置每种模型是否使用以及抽样次数。在右侧可以设置各模型的参数值。对于普通用户可以不用关心这些设置。

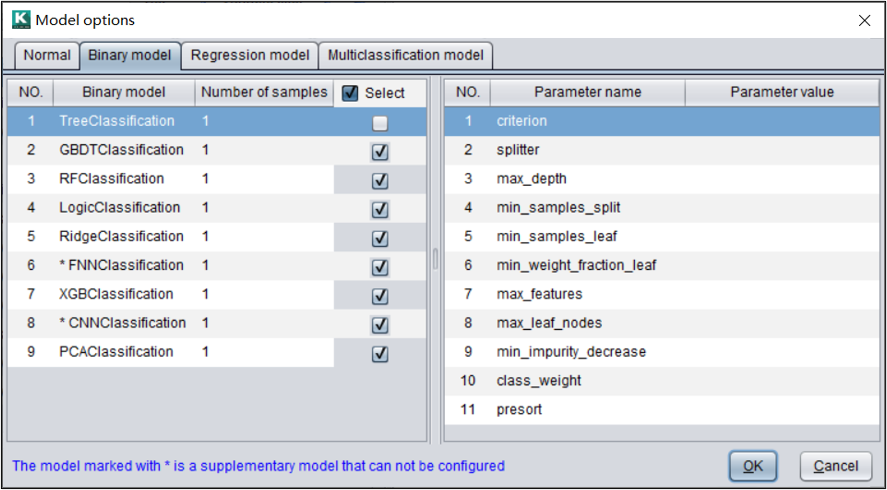
类似的，我们可以设置回归模型和多分类模型是否使用，以及各自的参数。

各模型参数的详细文档：《建模文档》

05模型表现

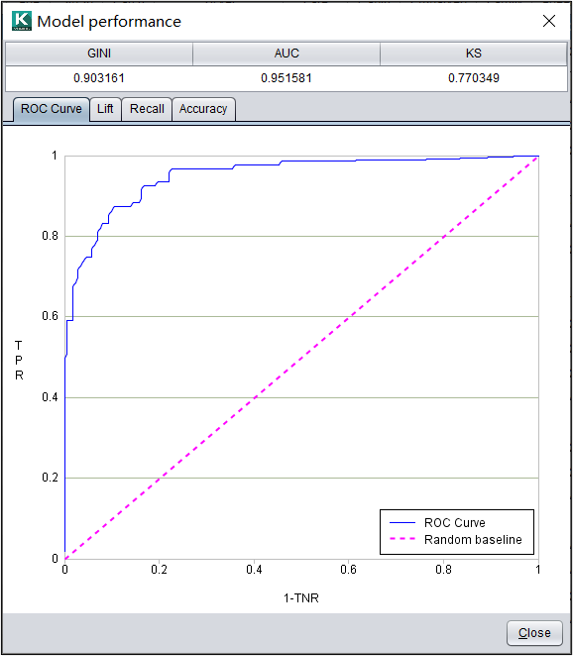
1. 模型表现

分类模型：评价指标

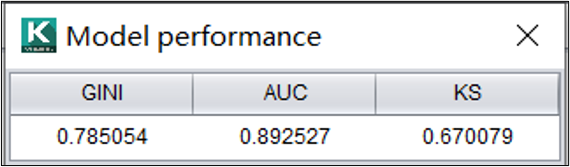
智能建模提供了分类模型常用的3个评价指标：

评价指标	描述
GINI	GINI指数在数值上等于2*AUC-1，用于表征模型对正负样本的区分能力。
AUC	AUC相当于ROC曲线下的面积。AUC值越大表示模型越好。
KS	KS值用于衡量模型区分正负样本的能力。KS值越大，模型区分正负样本的能力越强。

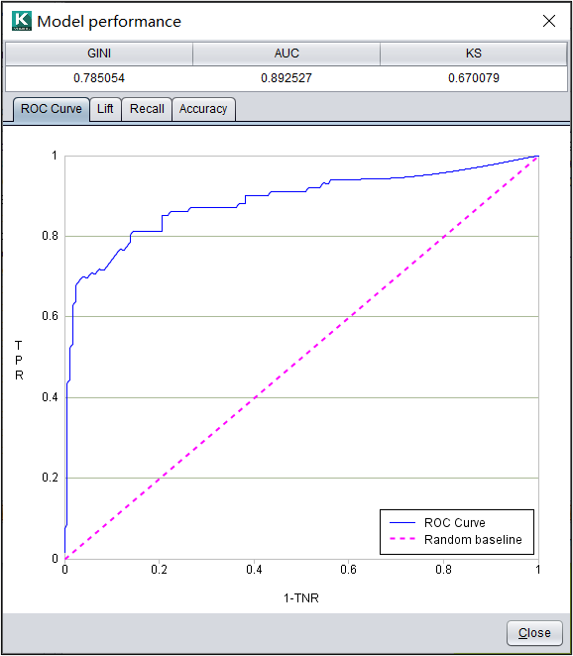
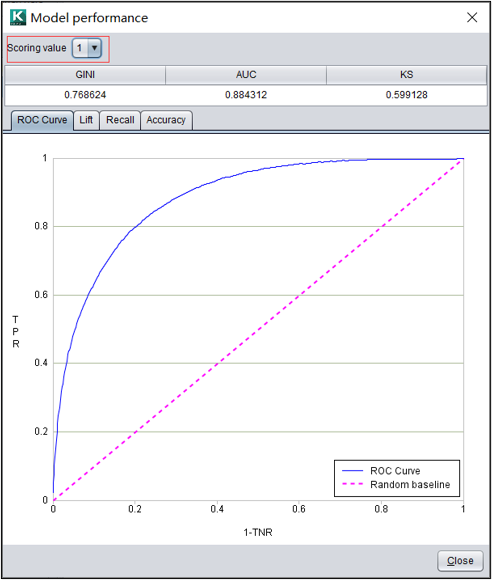
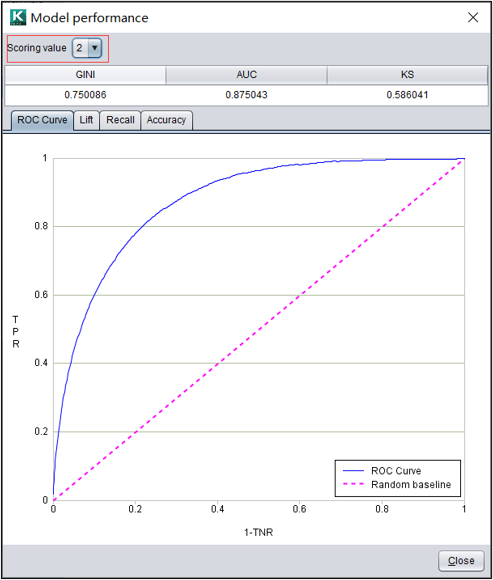
分类模型：ROC曲线

ROC曲线是真正类率与"1-真负类率"的关系图。ROC曲线可以被视为评估给定模型所有可能决策性能的可视化显示。

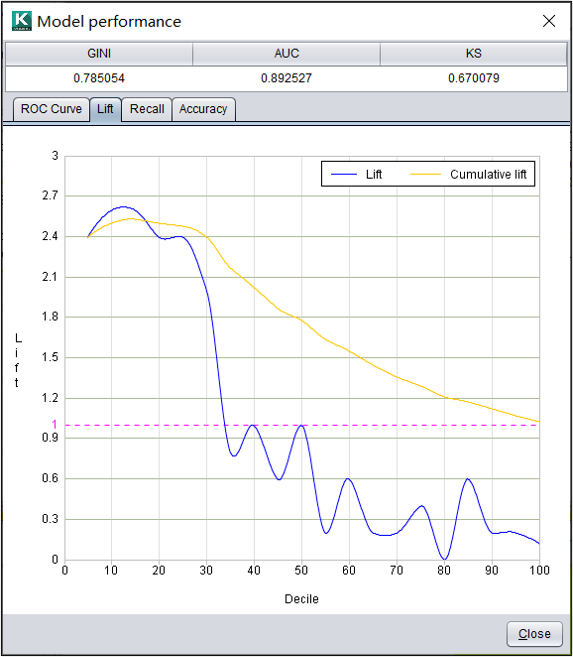
分类模型：提升度

提升度（Lift）表示使用关联规则可以提升的倍数，是置信度与期望置信度的比值。

提升度特别适合有针对性的市场营销等场景。

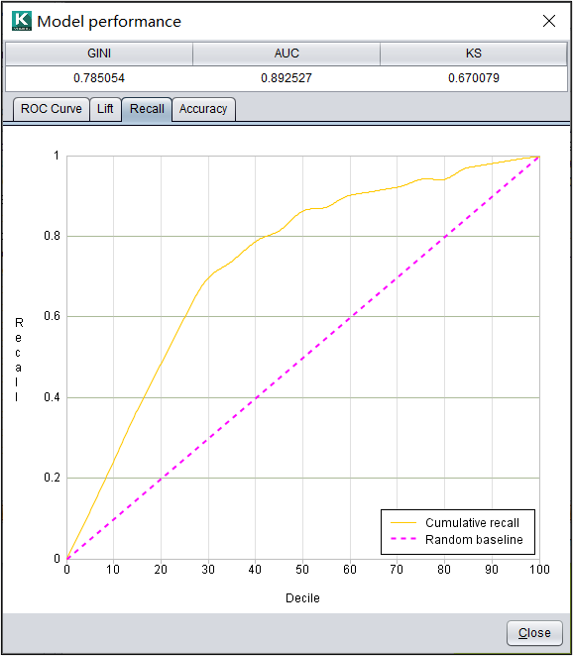
分类模型：查全率

查全率图显示模型找到正样本的情况，主要应用在数据不平衡的场景。累计查全率是各组累计正样本数与总正样本数的比值。

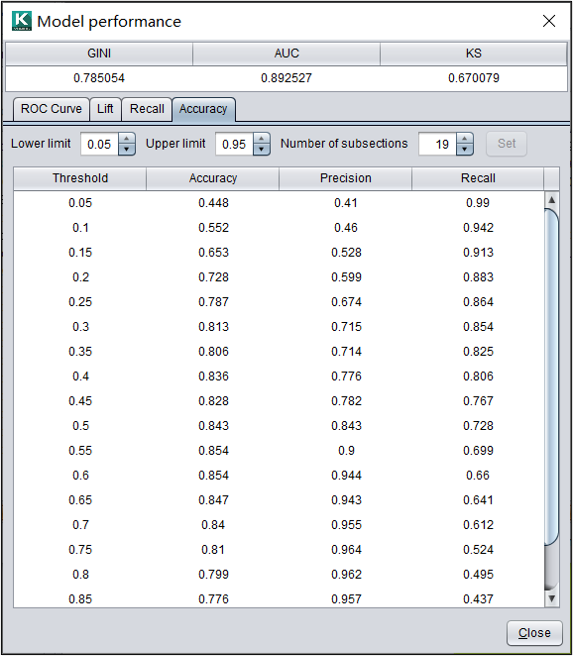
分类模型：准确率表

阈值：用来区分正负样本的值。
准确率：预测正确的样本占所有样本的比率。
精确率：预测为正样本的结果中，预测正确的比率。
查全率：正确预测正样本的数量，在所有正样本中的比率。

多分类模型

目标变量是分类变量时，模型表现通过切换预测值查看每个分类的模型表现。

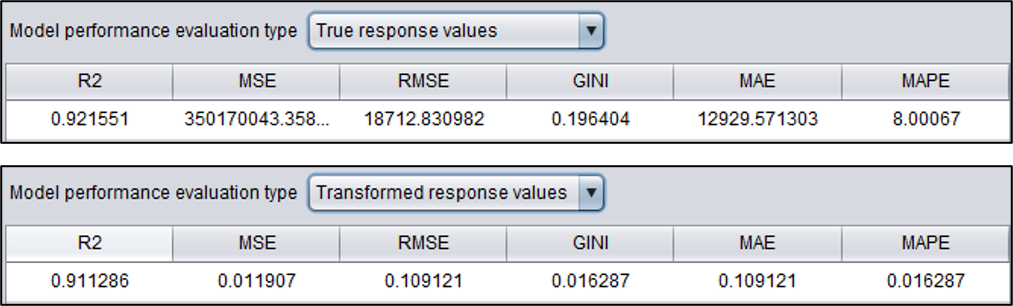
回归模型：真实值和转换值

回归模型的表现，分为真实值表现和转换值表现（对数据预处理后的数值）。真实值看起来比较直观，而转换值对于模型表现的评估更加准确。

回归模型：评价指标

智能建模提供了回归模型常用的6个评价指标：

评价指标	描述
R²	R²是预测值与观测值的误差平方和与观测值和观测均值之差的平方和的比值。
MSE	预测值与真实值偏差的平方和的平均数。
RMSE	MSE的平方根。数量级与真实值相同。
GINI	预测值与真实值偏差的绝对值的平均数。
MAE	预测值与真实值偏差的绝对值的平均数。
MAPE	预测值与真实值偏差比真实值的绝对值的平均数。

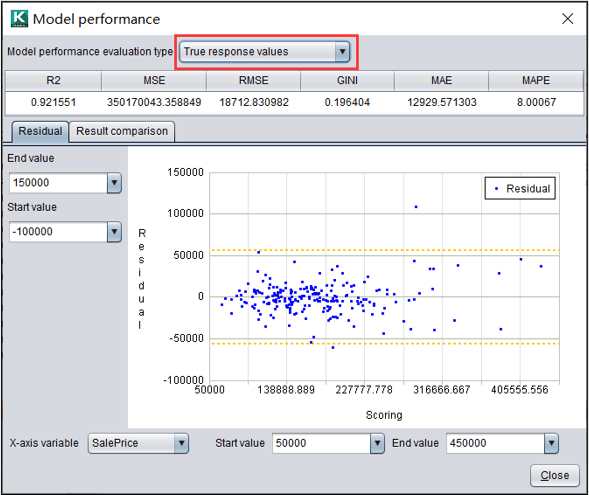
回归模型：残差图

残差是观察值与预测值之差。残差图是以残差为纵轴，以任一数值变量为横轴的散点图。图中黄线为三倍RMSE。

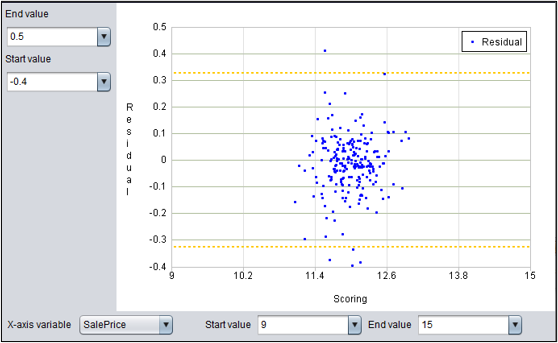
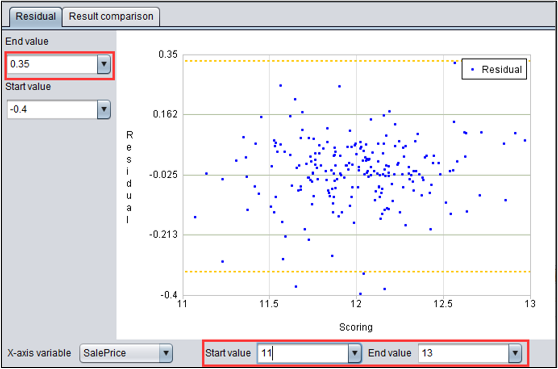
可以调整横轴变量和横纵轴的数值范围进一步查看。

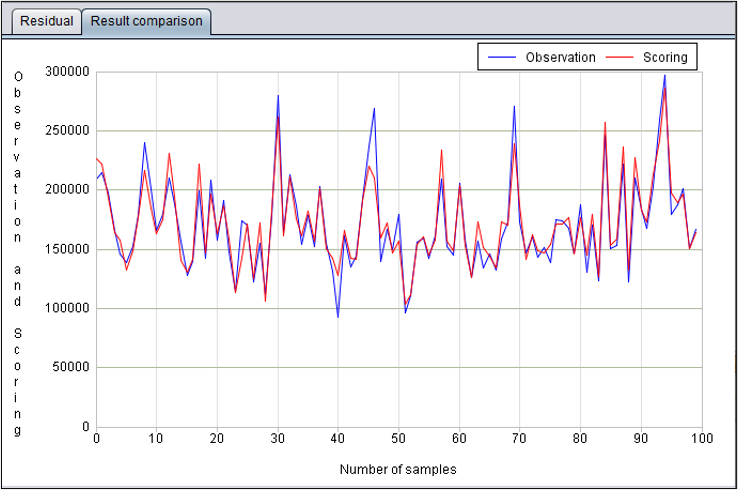
回归模型：结果对照图

结果对照图横轴为随机均分的样本，纵轴为对应的观察值和预测值。其中蓝色为观察值，红色为预测值。

2. 模型描述

模型描述列举了最终选出的模型组合以及每个模型的参数值。通过按钮可以将选中的模型参数复制到模型选项中，可以进一步优化模型参数。

Titanic模型最终使用的分类模型及参数

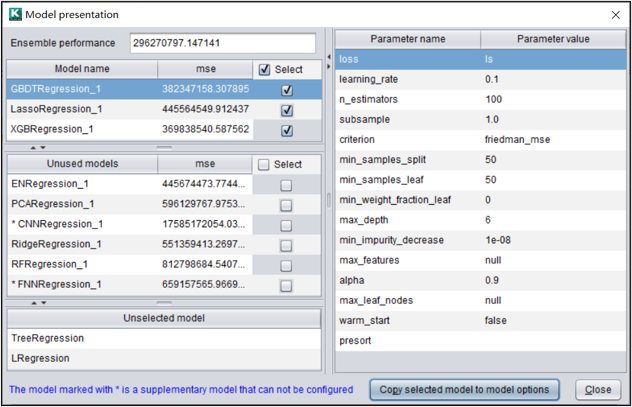
房价模型最终使用的回归模型及参数

3. 变量重要度

建模之后，可以得到本次建模时各变量的重要度信息。从titanic模型返回的重要度可以看到，性别（女士优先）和年龄范围（儿童优先）对于幸存最为重要。

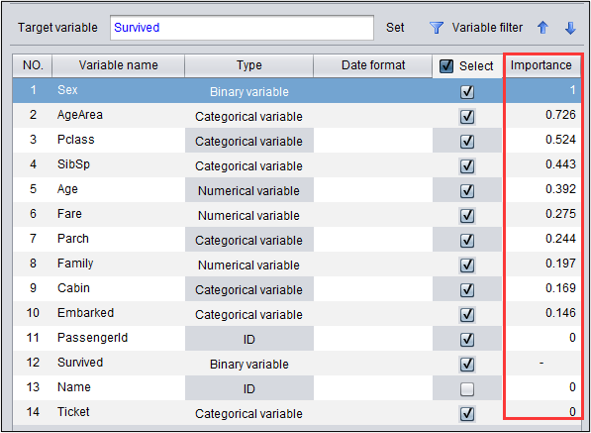
变量重要度的作用

参考变量重要度，有针对性的对数据重新处理。
使用重要度高的变量进行交互生成衍生变量，如路程/时间=速度，速度*时间=路程等重新建模。
参考变量重要度，有针对性的对客户进行建议。

06预测

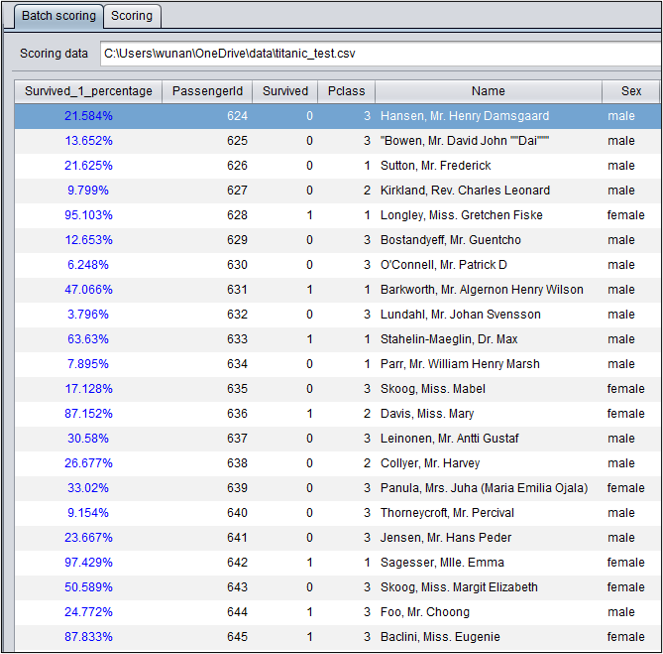
1. 批量预测

创建模型以后，可以使用测试数据进行预测。

对于二分类模型，第一列是目标变量为正样本的概率。

以titanic为例，预测624号乘客幸存的概率为21.584%。

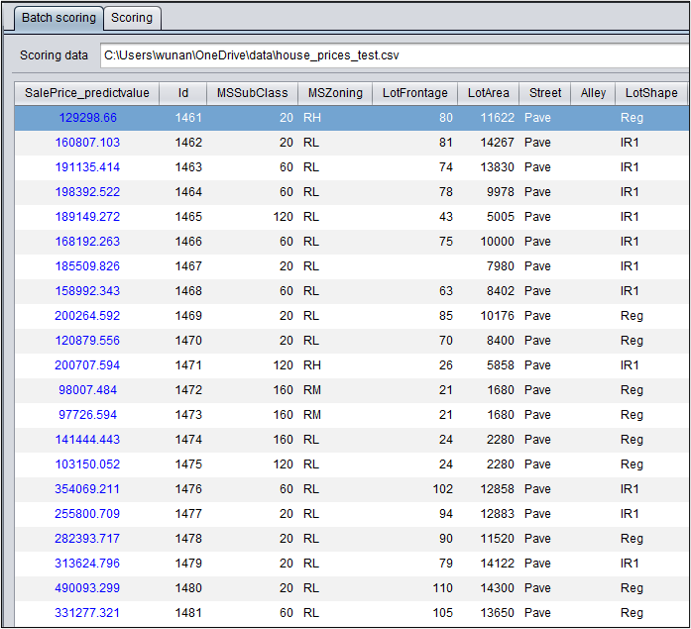
对于回归模型，第一列是对目标变量的预测值。

以房价预测为例，预测1461号房屋的价格为129298.66。

目标变量是分类变量时，预测后显示每个目标分类值的概率（总和为1）。例如第一条记录，目标值为2的概率最高，为97.402%。

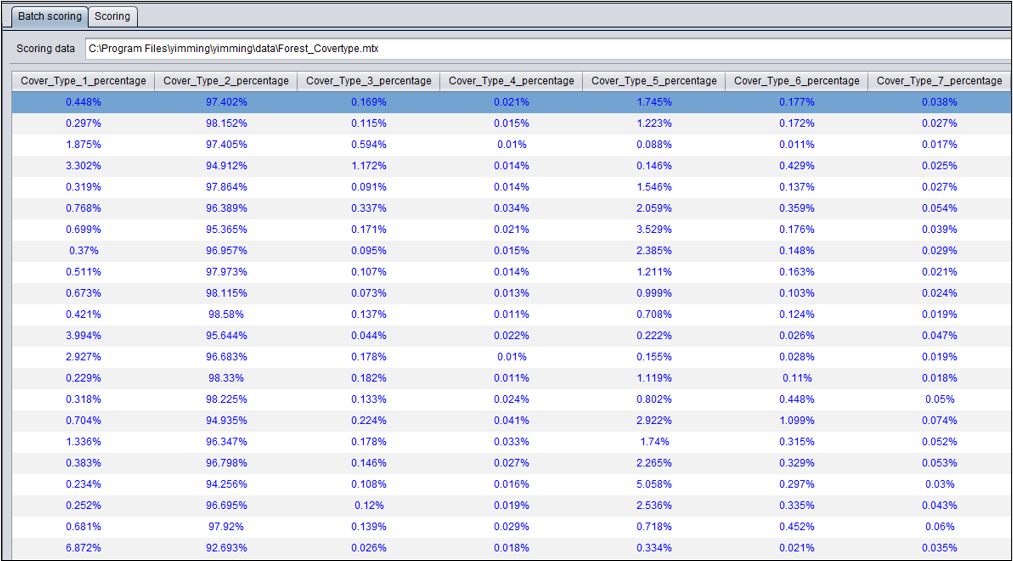
通常预测数据中是不包含目标变量的。

当预测数据中包含目标变量时，可以根据预测结果计算模型表现，用来评估模型。

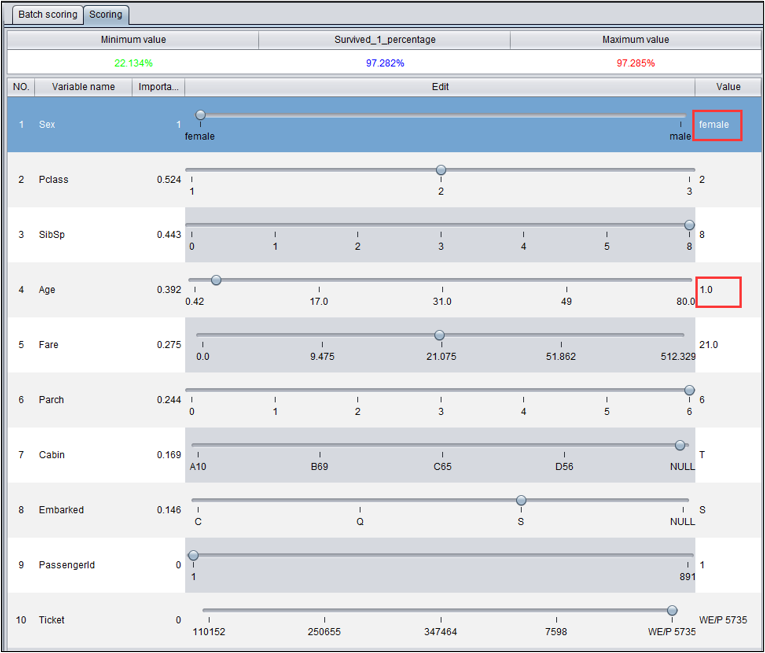
2. 单条预测

单条预测通过拖拽方式修改变量值，即时查看预测结果。

变量是按重要度降序排列的，通常靠前的变量对于预测结果的影响更大。可以看到年龄较小的女性幸存率很高。

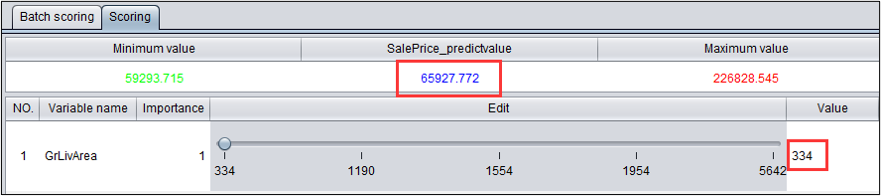
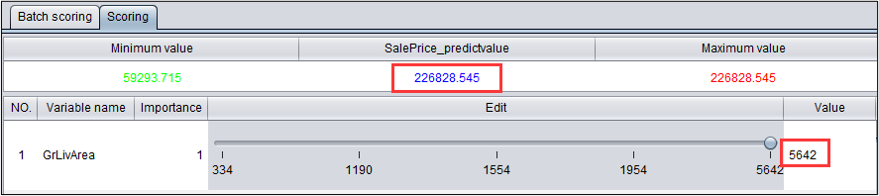
对于房价预测模型，可以看到当房屋地下室面积从334拖拽到5642时（其他变量没有改变），房价有了大幅提升。

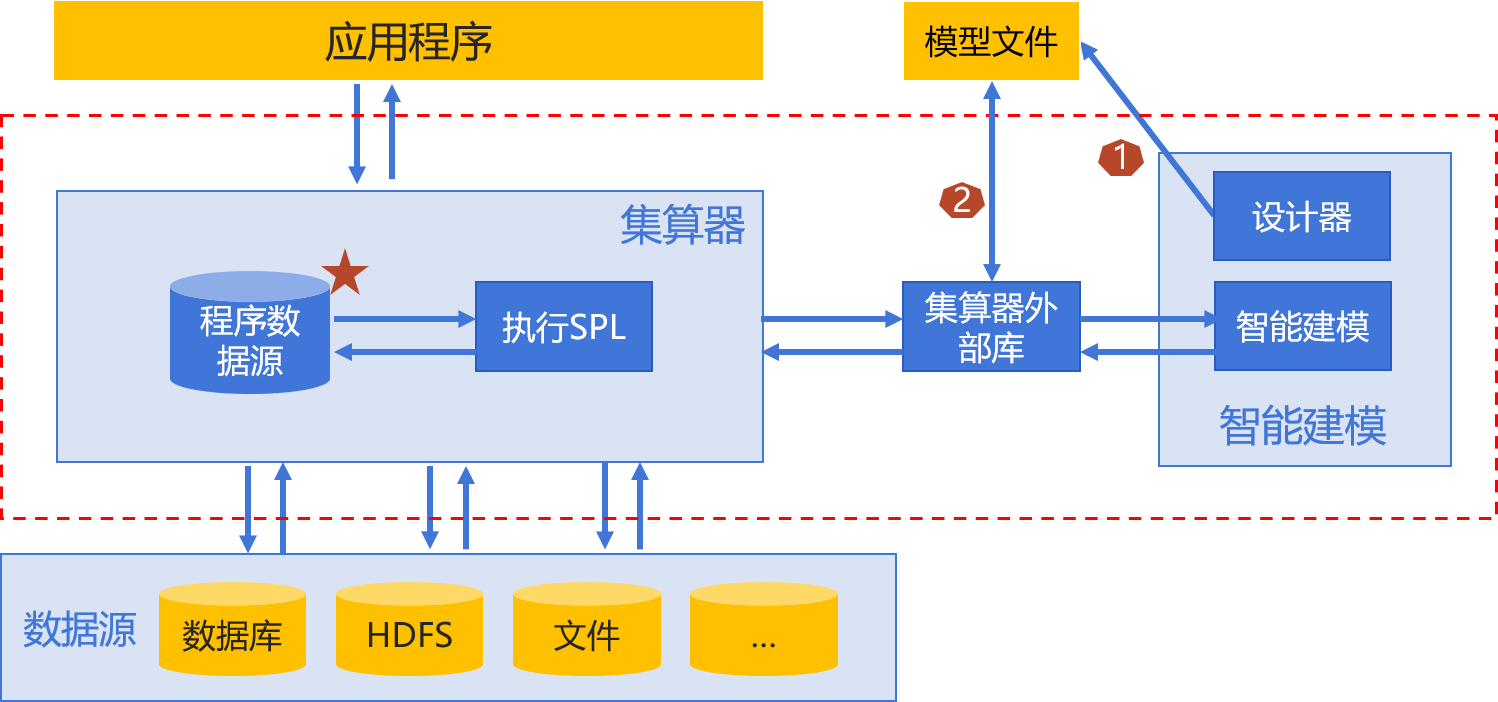
07集成方案

集算器外部库

集算器外部库提供了智能建模的接口函数，可以通过SPL调用。建模的SPL：

	A	B
1	=file("titanic_train.csv").cursor@cqt()	/创建训练数据游标
2	=ym_env()	/初始化环境
3	=ym_model(A2,A1)	/加载数据
4	=ym_target(A3, "Survived")	/设置目标变量
5	=ym_build_model(A3)	/执行建模
6	=ym_save_pcf(A5,"titanic.pcf")	/保存模型文件
7	=ym_json(A5)	/导出模型信息为json串
8	=ym_importance(A5)	/获取变量重要度
9	=ym_present(A5)	/获取模型描述
10	=ym_performance(A5)	/获取模型表现
11	>ym_close(A2)	/关闭

A7

值
{"Importance":{"PassengerId":0,"Pclass":0,"Sex":0,""Age":0.433191…

A8

Name	Importance
PassengerId	0.0
Pclass	0.0
…	…

A9

name	value	properties
XGBClass…	0.815	[[max_delt...
XGBClass…	0.777	[[max_delt...
…	…	…

A10

Name	Value
GINI	0.617
AUC	0.808
…	…

详细信息可以查看：《SPL实现自动建模和预测》

模型创建以后（也可以使用智能建模设计器创建的模型），可以通过SPL调用智能建模外部库进行预测。预测的SPL：

	A	B
1	=ym_env()	/初始化环境
2	=ym_load_pcf("titanic.pcf")	/加载模型文件
3	=file("titanic_test.csv").import@cqt()	/加载预测数据
4	=ym_predict(A2,A3)	/执行预测，返回预测结果对象
5	=ym_result(A4)	/获取预测结果序表
6	=ym_json(A4)	/预测数据不少于20条批量预测时，会根据预测数据评估导出模型表现json信息。
7	>ym_close(A1)	/关闭

A5

PassengerId	Survived	Pclass	Name	Sex	…
624	0	3	Hansen,…	male	…
625	0	3	Bowen, …	male	…
626	0	1	Sutton, …	male	…
627	0	2	Kirkland…	male	…
…	…	…	…	…	…

A6

值
{"Model-Performance":"{\"GINI\":0.8369670542635659,\"AUC\":0.9184835271317829,\"KS\":0.6867732558139534,\"ROC-Data\":[\"{\\\"1-specificity\\\":\\\"0.0\\\",\\\"sensitivity\\\":\\\"0.020833333333333332\\\"}\",\"{\\\"1-…

集成框架

创建模型有两种方式：

使用智能建模设计器创建模型文件。
通过SPL调用集算器外部库建模。

这里的程序数据源是指以SPL程序作为数据源。

本页目录